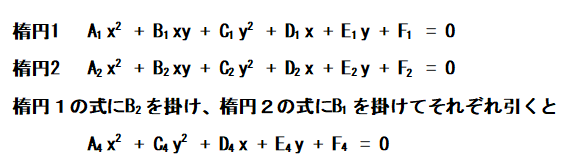楕円同士の交点 その４
楕円同士の交点の求め方についての質問がインターネットに載っているのですが、その中に面白い回答が有ったので、検討をしてみました。
そこでの楕円の方程式は
楕円1 A(x-a)2 + 2Bxy + C(y-c)2 = 1
楕円2 D(x-d)2 + 2Exy + F(y-f)2 = 1
の二つの楕円の交点と、交点があるかどうかの判別です。
楕円1にEをかけて、楕円2にＢをかけて差分をとって、xyを消去してはとあったのですが、基本的に楕円の交点の有無と交点の座標は連立方程式を解くか、片方を円に変換して、楕円の方の楕円上の座標を計算して円との距離から交点があるかどうか判別し交点の座標を取得するしか現在は方法がありません。
上記の式は、一般の二元二次式に変換ができるので下記のものと等価です。
二元二次式にすれば、楕円の角度、長半径、短半径、中心座標の計算が可能となります。
A1=A, B1=2B, C1=C, D1=-2Aa, E1=-2Cc, F1=Aa2 + Cc2 - 1
A2=D, B2=2E, C2=F, D2=-2Dd, E2=-2Ff, F2=Dd2
+ Ff2 - 1
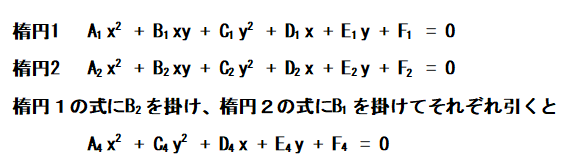
二つの楕円の二元二次式からBxyを消去して新しい楕円の二元二次式を得るものです。
得られた楕円は、角度の無い標準の楕円となりますが、必ずしも楕円とはならずに双曲線となる場合もあります。
Bxyを消去した、二元二次方程式と、楕円１、或いは楕円２との連立方程式を解いてみましたが、Bxyを消去した事により、二つの楕円の楕円比が等しくて楕円の角度が等しい場合、連立方程式が解けない事が分かりました。
この時は、楕円比と角度が同じなので、円に変換して、二つの円の交点として計算すれば交点が求められます。
連立方程式を解くときは、Cy^2を消去するのですが、Cy^2の消去により、軸対称のとき連立方程式が解けないので、更に新しい解けない条件が追加される事になります。
とにかくプログラムを作って、作図してみました。
遊びとしては良いですが、無駄な作業です。
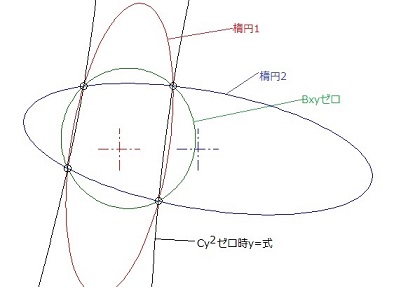Bxyを消去した場合、角度がなくなるので、楕円は０°か９０°の楕円になります。
場合によっては、次の図様な双曲線になります。
二つの楕円の角度方向(回転)の座標変換を行う事により、双曲線にならない条件が必ず存在します。
交点計算のプログラムでは、軸対象、双曲線を避ける角度に座標変換をして計算する場合、楕円の角度の変更が必要で、座標変換をして計算し、元へ戻しているため、作図されるBxyを消去した楕円は、座標変換した分の角度のついた楕円として作図されます。
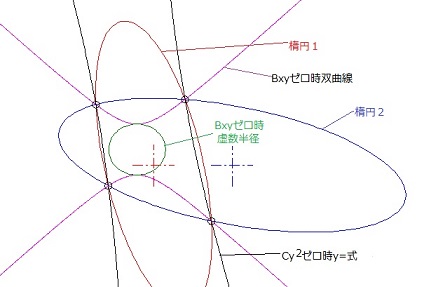双曲線になった場合のサンプルです。
半径が虚数になるのですが、実数として作図すると、双曲線に接する楕円として作図されます。
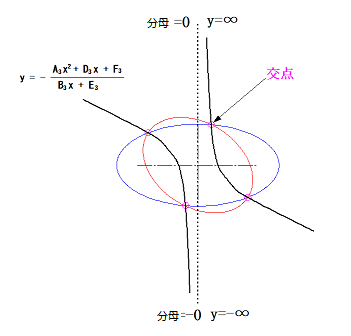
Cy^2を消去した式で作図すると、分母が０(ゼロ)になる点があるので注意が必要です。
プログラム
unit Main;
interfac
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, math;
type
TForm1 = class(TForm)
Panel1: TPanel;
Ellipse1Box: TGroupBox;
radius_a1_Edit: TLabeledEdit;
radius_b1_Edit: TLabeledEdit;
Center_x1_Edit: TLabeledEdit;
Center_y1_Edit: TLabeledEdit;
angle_q1_Edit: TLabeledEdit;
Ellipse2Box: TGroupBox;
radius_a2_Edit: TLabeledEdit;
radius_b2_Edit: TLabeledEdit;
Center_x2_Edit: TLabeledEdit;
Center_y2_Edit: TLabeledEdit;
angle_q2_Edit: TLabeledEdit;
Panel2: TPanel;
SelectBtn: TBitBtn;
Image1: TImage;
Image2: TImage;
Timer1: TTimer;
AutoBtn: TButton;
StepBtn: TButton;
CheckBox1: TCheckBox;
pEdit: TLabeledEdit;
EchkBox: TCheckBox;
CheckBox2: TCheckBox;
NoXYBox: TCheckBox;
CY2ZeroBox: TCheckBox;
firstBox: TCheckBox;
crosspBox: TCheckBox;
Label1: TLabel;
KcchEdit: TLabeledEdit;
procedure FormCreate(Sender: TObject);
procedure SelectBtnClick(Sender: TObject);
procedure AutoBtnClick(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure StepBtnClick(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear;
function Dist(x1, y1, x2, y2 : Extended): Extended;
function Angle(dx, dy: Extended): Extended;
procedure LineSub(Tcv: TCanvas; px1, py1, px2, py2: Extended);
procedure pitchControl(NLine, LW: integer);
procedure LineSubPitch(Tcv : TCanvas; Ln: integer; var i: integer; var d1: Extended; px1, py1, px2, py2:Extended);
function angleSe(a, b, rad: Extended): Extended;
procedure EllipseEx(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: Extended);
procedure quadratic_transform(a, b, x, y, qdeg: Extended; var A0, B0, C0, D0, E0, F0: Extended);
procedure inputdata_drawing;
function cross_calc: boolean;
function cross_quadratic(a, b, c, d, e: Extended; var x1, x2, x3, x4: Extended): byte;
procedure trance(Xn, Yn, defQ, xo1, yo1: Extended; var x, y: Extended);
procedure StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: Extended; sf: boolean);
function elementsCalc(A,B,C, D,E,F: Extended; var X, Y, Ar, Br, Q: Extended): boolean; // 各要素計算
procedure AutoCheckRoot;
Procedure WMSysCommand(var Messages: TWMSysCommand);message WM_SysCommand;
function anglecheck(saq, dq: Extended): Extended;
procedure hyperbola(A4, B4, C4, D4, E4, F4, Qs: Extended);
procedure Secondary_curve(A3, B3, D3, E3, F3, Qs: Extended);
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of Extended; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
LPitch : array of TLinePitch; // 線種用 (線ピッチ)
VPitch : array[0..PitchN] of Extended; // 線幅による線ピッチ設定用
magnification : Extended;
ar1, ar2 : Extended;
br1, br2 : Extended;
xo1, xo2 : Extended;
yo1, yo2 : Extended;
q1, q2 : Extended;
shift_x : Extended;
shift_y : Extended;
d01 : Extended;
d0p : integer;
TimF : boolean;
xb1, xb2 : Extended;
yb1, yb2 : Extended;
dfQ : Extended;
scale : Extended;
KCCH : Extended;
const
draw_margin = 30; // 左右上下作図マージン
//--------------------------------------------
// システムコマンド取得
// フォームクローズボタンクリック処理
// 自動計算for ループから抜けるのに必要です
//--------------------------------------------
procedure TForm1.WMSysCommand(var Messages: TWMSysCommand); // フォームのborder Close ボタンのみ有効の場合
begin
case (messages.CmdType and $FFF0) of
SC_CLOSE: begin
Timer1.Enabled := False; // タイマー停止
inherited; // デフォルト処理
end;
else
inherited; // 指定以外はデフォルト処理
end;
end;
//-----------------------------
// 表示画像消去
//-----------------------------
procedure TForm1.imageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
image2.Canvas.FillRect(Rect(0, 0, image2.Width, image2.Height));
end;
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
// LW 線幅
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//----------------------------
// 作図用 二点間線引き
//----------------------------
procedure TForm1.LineSub(Tcv: TCanvas; px1, py1, px2, py2: Extended);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
Tcv.MoveTo(x1, y1);
Tcv.LineTo(x2, y2);
end;
//----------------------
// 距離（長さ）を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : Extended): Extended;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) ;
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0～2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: Extended): Extended ;
var
r : Extended ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//--------------------------------------
// 線分の表示・サブ２：線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Tcv: TCanvas; Ln: integer; var i: integer; var d1: Extended; px1, py1, px2, py2:Extended);
var
x1, y1, x2, y2 : Extended;
a, sa, ca, d, p : Extended;
PenStyle : TPenstyle;
begin
PenStyle := Tcv.Pen.Style; // 線種バックアップ
Tcv.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(Tcv, px1, py1, px2, py2);
Tcv.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1 ; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca ; // 新しい位置計算
y2 := y1 + p * sa ;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(Tcv, x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p ; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Tcv.Pen.Style := PenStyle; // 線種戻し
end;
//------------------------------------------
// 楕円の開始角を 基礎円の開始角に変換
//------------------------------------------
function TForm1.angleSe(a, b, rad: Extended): Extended;
const
KMIN = 0.00000001;
var
l : Extended;
begin
// 90°, 270°, 0°, 180° 360°近傍は計算しない
if (abs(rad - pi / 2) < KMIN) or (abs(rad - pi - pi / 2) < KMIN)
or (abs(rad) < KMIN) or (abs(rad - pi) < KMIN) or
(abs(rad - pi * 2) < KMIN)
then begin
result := rad;
exit;
end;
// 底辺の長さ計算 ( b / a の値がいつも正の値なので元の角度によって角度を補正)
// 分母がゼロに近くなる時もあるので、判別が不要なarctan2を使用します
l := b / a / tan(rad);
// 180°以下だったら
if rad < pi then
result := arctan2(1, l)
else
// 360°以下だったら
if rad < pi * 2 then
result := arctan2(1, l) + pi
// 360°を超えていたら
else
result := arctan2(1, l) + pi * 2;
end;
//-------------------------------------------------------------
// 直線の描画
// 直線の開始はsfをTrueにします。
// つながった直線、折れ線を描画する場合は、sfをFalseに
//-------------------------------------------------------------
procedure TForm1.StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: Extended; sf: boolean);
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// y方向変換
ys := h - ys;
ye := h - ye;
if sf then begin
d01 := 0;
d0p := 0;
end;
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
d0p, // セグメント位置
d01, // 長さ
xs, // 始点X
ys, // 始点Y
xe, // 終点X
ye // 終点Y
);
end;
//---------------------------------------
// 楕円の描画
// Windows為ののy方向変換は,このルーチンで行います。
// tcv 描画キャンバスの指定
// h キャンバスの高さ
// lf 線の種類
// lw 線の幅
// lc 線の色
// a 半径a
// b 半径b
// x 中心位置 x
// y 中心位置 y
// rq 楕円の角度
// sq 描画開始角
// eq 描画終了
//---------------------------------------
procedure TForm1.EllipseEx(Tcv : TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: Extended);
var
sqrad, eqrad : Extended;
qrad : Extended;
Ssqrad, Seqrad : Extended;
sp : integer;
dq : Extended;
d1 : Extended;
dp : integer;
xf, yf : Extended;
rdist, nrad : Extended;
px1, py1 : Extended;
px2, py2 : Extended;
i : integer;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// y方向変換
y := h - y;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
// 分割数 半径に応じて調整
sp := abs(round(sqrt(a + b) * 4)); // 分割数
if sp > 10000 then sp := 10000;
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp < 1 then sp := 1;
if sp > 10000 then sp := 10000;
dq := (Seqrad - Ssqrad) / sp; // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp < 1 then sp := 1;
if sp > 10000 then sp := 10000;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
xf := cos(Ssqrad) * a; // 基本楕円座標X スタート座標
yf := sin(Ssqrad) * b; // 基本楕円座標y スタート座標
nrad := arctan2(yf, xf) + qrad; // 新しい角度 回転角加算
rdist := sqrt(xf * xf + yf * yf); // 中心と楕円座標の距離
px1 := cos(nrad) * rdist + x; // 開始座標X
py1 := sin(nrad) * -rdist + y; // 開始座標Y -rdistはY座標反転の為
// WindowはY座標方向が逆のため
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
xf := cos(Ssqrad + dq * i) * a;
yf := sin(Ssqrad + dq * i) * b;
nrad := arctan2(yf , xf) + qrad;
rdist := sqrt(xf * xf + yf * yf);
px2 := round(cos(nrad) * rdist + x); // 終点座標X
py2 := round(sin(nrad) * -rdist + y); // 終点座標Y
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
//=====================================================================================================
//-------------------------------------------------
// 楕円の方程式 二次方程式への変換
// AX^2 + BXY + CY^2 + DX + EY + F の A,B,C,D,E,F
//-------------------------------------------------
procedure TForm1.quadratic_transform(a, b, x, y, qdeg: Extended; var A0, B0, C0, D0, E0, F0: Extended);
var
Q : Extended;
sin_Q, cos_q : Extended;
ah2, bh2 : Extended;
sinh2, cosh2 : Extended;
sincosQ : Extended;
xh2, yh2, xy : Extended;
begin
Q := qdeg / 180 * pi; // ラジアン単位に変換
sin_Q := sin(Q);
cos_Q := cos(Q);
ah2 := a * a;
bh2 := b * b;
sinh2 := sin_Q * sin_Q;
cosh2 := cos_Q * cos_Q;
sincosQ := sin_Q * cos_Q;
xh2 := x * x;
yh2 := y * y;
xy := x * y;
A0 := cosh2 / ah2 + sinh2 / bh2;
B0 := 2 * (1 / ah2 - 1 / bh2) * sincosQ;
C0 := sinh2 / ah2 + cosh2 / bh2;
D0 := -2 * ((x * cosh2 + y * sincosQ) / ah2 + (x * sinh2 - y * sincosQ) / bh2);
E0 := -2 * ((x * sincosQ + y * sinh2) / ah2 + (y * cosh2 - x * sincosQ) / bh2);
F0 := (xh2 * cosh2 + 2 * xy * sincosQ + yh2 * sinh2) / ah2
+ (xh2 * sinh2 - 2 * xy * sincosQ + yh2 * cosh2) / bh2
- 1;
end;
//----------------------------------------------------------------------------
// 二元二次の値を楕円式に変換
// 半径が虚数になるときFalseを返します。
// 半径が虚数の場合符号をとってルートを開き値をかえします。
// 虚数と実数の間に半径が無限大になる点が存在しますがその時は値の制限をします。
// 値の制限をしても交点の計算には使用されないので問題ありません。
//----------------------------------------------------------------------------
function TForm1.elementsCalc(A, B, C, D, E, F: Extended; var X, Y, Ar, Br, Q: Extended): boolean;
const
Kxy = 1E-20;
Kab = 1E-15;
var
xy : Extended;
cosQ, sinQ : Extended;
at, bt, kd : Extended;
af, bf : boolean;
LL : string;
Xout, Yout : Extended;
begin
// 楕円の各係数計算
Result := true;
xy := (B * B - 4 * A * C);
if abs(xy) < Kxy then xy := sign(xy) * Kxy; // ゼロでの除算防止
X := (2 * D * C - E * B) / xy; // 原点からのX方向移動量
Y := (2 * A * E - D * B) / xy; // 原点からのy方向移動量
Q := - arctan2(B, C - A) / 2; // 標準楕円からの回転角
cosQ := cos(Q);
sinQ := sin(Q);
at := A * cosQ * cosQ + B * cosQ * sinQ + C * sinQ * sinQ;
bt := A * sinQ * sinQ - B * cosQ * sinQ + C * cosQ * cosQ;
af := False;
kd := A * X * X + B * X * Y + C * Y * Y + D * X + E * Y + F;
if at * KD >= 0 then af := true; // 半径虚数
bf := False;
if bt * KD >= 0 then bf := true; // 半径虚数
image2.Canvas.TextOut(10, 325, 'Bxyゼロ時の図形情報');
// 半径が虚数の時
if af or bf then begin
Result := false; // 双曲線フラグセット
image2.Canvas.TextOut(20, 340, '双曲線です。');
end
else
image2.Canvas.TextOut(20, 340, '楕円近似です。');
// 半径が無限大になるのを防止しま ゼロでの除算暴防止
if abs(at) < Kab then at := Kab;
if abs(bt) < Kab then bt := Kab;
// 半径は絶対値を返します
// 虚数の時は虚数フラグで返します。
// 双曲線の時、二つの双曲線の中心位置を中心とした双曲線に接する楕円となります。
Ar := sqrt(abs(Kd / at)); // 半径a
Br := sqrt(abs(kd / bt)); // 半径b
if Result = True then begin
// 計算座標を原点座標に戻し
trance(X, Y, dfQ, xo1, yo1, Xout, Yout);
// 計算原点が楕円1なので楕円1中心座標で修正
Xout := Xout + xb1;
Yout := Yout + yb1;
LL := '半径 ａ＝ ' + floatTostrF(Ar / scale, ffGeneral, 8, 3);
if af then LL := LL + ' ｉ';
image2.Canvas.TextOut(30, 355, LL);
LL := '半径 ｂ＝ ' + floatTostrF(Br / scale, ffGeneral, 8, 3);
if bf then LL := LL + ' ｉ';
image2.Canvas.TextOut(30, 370, LL);
image2.Canvas.TextOut(30, 385, '中心座標 Ｘ＝ ' + floatTostrF(Xout / scale, ffFixed, 8, 3));
image2.Canvas.TextOut(30, 400, '中心座標 Ｙ＝ ' + floatTostrF(Yout / scale, ffFixed, 8, 3));
// image2.Canvas.TextOut(30, 415, '角度 θ＝ ' + floatTostrF(Q / pi * 180, ffFixed, 10, 3)+'°');
end;
Q := Q / Pi * 180;
end;
//----------------------------------------------------------
// CY^2のC消去式作図
// y = - (A3x^2 + D3x + F3)/(B3x + E3)
// xの値を代入しyの値を求め作図します。
// 変曲点がありその部分は特に細かく分割して計算します。
//----------------------------------------------------------
procedure TForm1.Secondary_curve(A3, B3, D3, E3, F3, qs: Extended);
var
I, M, J : integer;
Xs, Xe, dx, ddx : Extended;
X1, Y1 : Extended;
X2, Y2 : Extended;
XY, QQ : Extended;
LF, DF : boolean;
CX : Extended;
Mr : Extended;
Ys, Ye, Bx : Extended;
// 座標変換と２点間線引
procedure Line_curve;
begin
QQ := arctan2(Y2, X2);
XY := sqrt(X2 * X2 + Y2 * Y2);
X2 := (XY * cos(QQ - qs) - shift_x) * magnification + draw_margin;;
Y2 := (XY * sin(QQ - qs) - shift_y) * magnification + draw_margin;
if LF then StraightLineDraw(image1.Canvas, image1.Height, 3, 1, clBlack, X1, Y1, X2, Y2, False);
X1 := X2;
Y1 := Y2;
LF := true;
end;
// Yの値を計算し範囲内か確認範囲内なら作図
procedure Line_make;
begin
if CX <> 0 then begin
Y2 := - (A3 * X2 * X2 + D3 * X2 + F3) / CX;
if (Y2 > Ys) and (Y2 < Ye) then Line_curve // ２点間線引
else LF := False;
end
else LF := False;
end;
begin
// 最大半径
Mr := ar1;
if br1 > Mr then Mr := br1;
if ar2 > Mr then Mr := ar2;
if br2 > Mr then Mr := br2;
Mr := Mr * 1.5;
// 作図範囲設定
Xs := (- Mr - abs(xo2));
Xe := (abs(xo2) + Mr);
Ys := (- Mr - abs(yo2));
Ye := (abs(yo2) + Mr);
Bx := (Ys + Ye) / 2;
Ys := (Ys - BX) * 2 + BX;
Ye := (Ye - BX) * 2 + BX;
// Xの値設定用微小x
dx := (Xs - Xe) / 2000; // 微小x
// Xの値設定用極小x
ddx := dx / 200; // 極小x
// 計算の範囲
M := -2000;
X1 := 0; // 初期化
Y1 := 0; // 初期化
LF := False;
DF := True; // 一度だけ実行する為のフラグ設定
X2 := M * dx;
BX := (B3 * X2 + E3); // 変曲点検出用
// Xの値からYの値を計算し線を引きます
for I := M to -M do begin
X2 := I * dx;
CX := (B3 * X2 + E3);
// 値の変曲点だったら 極小ddxで計算
if (CX * BX < 0) and DF then begin
for J := 0 to 401 do begin
X2 := (I - 2) * dx + J * ddx;
CX := (B3 * X2 + E3);
Line_make; // 線引
end;
DF := False; // 一度実行済フラグ設定
end
else
Line_make; // 線引
end;
end;
//------------------------------------------------------------------
// 双曲線作図
// Ax^2 + Bxy + Cy^2 + Dx + Ey + F に x の値を代入しyの値を求めます
// ay^2 + by + c
// y = (-b + sqrt(b^2 - 4ac))/2/a
// y = (-b - sqrt(b^2 - 4ac))/2/a
// a = C
// b = Bx + E
// c = Ax^2 + Dx + F
// 此処ではB4はゼロです。
//------------------------------------------------------------------
procedure TForm1.hyperbola(A4, B4, C4, D4, E4, F4, Qs: Extended);
var
M : integer;
dx, XI : Extended;
X1, Y1 : Extended;
X2, Y2 : Extended;
a, b, c : Extended;
f : Extended;
Xs, Xe, XY : Extended;
QQ : Extended;
Lf : boolean;
Mr : Extended;
PMF : Boolean;
// 指定範囲双曲線作図
procedure hyperbolaLine;
var
I : integer;
begin
for I := M to -M do begin
XI := I * dx;
b := E4; // B4は常時ゼロ
// b := B4 * XI + E4;
c := A4 * XI * XI + D4 * XI + F4;
f := b * b - 2 * a * c;
if f >= 0 then begin
if PMF then Y2 := (-b - sqrt(f)) / a
else Y2 := (-b + sqrt(f)) / a;
QQ := arctan2(Y2, XI);
XY := sqrt(XI * XI + Y2 * Y2);
X2 := (XY * cos(QQ - qs) - shift_x) * magnification + draw_margin;;
Y2 := (XY * sin(QQ - qs) - shift_y) * magnification + draw_margin;
if LF then StraightLineDraw(image1.Canvas, image1.Height, 3, 1, clFuchsia, X1, Y1, X2, Y2, False);
X1 := X2;
Y1 := Y2;
LF := true;
end
else LF := False;
end;
end;
begin
// 半径の最大値検索
Mr := ar1;
if br1 > Mr then Mr := br1;
if ar2 > Mr then Mr := ar2;
if br2 > Mr then Mr := br2;
// Xの計算範囲設定
Xs := (- Mr - abs(xo2));
Xe := (abs(xo2) + Mr);
// 分割計算用微小x設定
dx := (Xs - Xe) / 1000;
M := -1000;
X1 := 0;
Y1 := 0;
a := C4 * 2; // 二次方程式の解の分母の設定
LF := False;
PMF := True; // 解のマイナス側計算フラグ
hyperbolaLine;
LF := False;
PMF := False; // 解のプラス側計算フラグ
hyperbolaLine;
end;
//-----------------------------------------------------
// 四次 二次方程式の解法 デカルトの方法
// 三次式は発生しません。
// ax^4 + bx^3 + cx^2 + dx + e = 0
// x の 値は 4個 又は 2個
// 虚数にならない X を フラグにして byteで返します
// x1 bit0 x2 bit1 x3 bit2 x4 bit3
//-----------------------------------------------------
function TForm1.cross_quadratic(a, b, c, d, e: Extended; var x1, x2, x3, x4: Extended): byte;
const
MINIMAM = 1E-15;
MAXMEMA = 1E-8;
EXD = 1E-7;
DBL = 1E-5;
var
A3, A2, A1, A0 : Extended;
b2, b1, b0 : Extended;
f0 : Extended;
e1, e0, e1s3, e0s2, e02s4, e13s27 : Extended;
e02s4pe13s27 : Extended;
r, rh1s3, cosQ, Q, cosQs3, sinQs3 : Extended;
u, v, wiupv, t, c1, c0 : Extended;
up, vm : string;
d1, d0, c1h2s4mc0, d1h2s4md0 : Extended;
xim1, xim2, xim3, xim4 : string;
KXYE : Extended;
begin
// 計算精度判別
KXYE := EXD;
U := 1 + 1.0E-17; // この計算Double だと桁落ちします表示は1で変わりません。
if U = 1 then KXYE := DBL;
// 初期化
Result := 0;
rh1s3 := 0;
sinQs3 := 0;
u := 0;
v := 0;
xim1 := '';
xim2 := '';
xim3 := '';
xim4 := '';
up := '…';
vm := '…';
// a=0 の場合は四次方程式でないので解法不可
if (abs(a) > MINIMAM) then begin
// x^4 + A3x^3 + A2x^2 + A1x + A0 = 0 に変換
A3 := b / a;
A2 := c / a;
A1 := d / a;
A0 := e / a;
// 四次式の解法
b2 := -3 / 8 * A3 * A3 + A2;
b1 := A3 * A3 * A3 / 8 - A3 * A2 / 2 + A1;
b0 := -3 / 256 * A3 * A3 * A3 * A3 + A3 * A3 * A2 / 16 - A3 * A1 / 4 + A0;
e1 := -b2 * b2 / 3 - 4 * b0;
e0 := -2 / 27 * b2 * b2 * b2 + 8 / 3 * b2 * b0 - b1 * b1;
e1s3 := e1 / 3;
e0s2 := e0 / 2;
e02s4 := e0s2 * e0s2;
e13s27 := e1s3 * e1s3 * e1s3;
e02s4pe13s27 := e02s4 + e13s27; // 判別式1
t := b2 * b2 - 4 * b0; // 判別式2
if (b1 <> 0) or (t < 0) then begin
if e02s4pe13s27 >= 0 then begin
u := -e0 / 2 + sqrt(e02s4pe13s27);
if u < 0 then begin // 負数の立方根対策
u := power(-u, 1/3);
u := -u;
end
else u := power(u, 1/3);
v := -e0 / 2 - sqrt(e02s4pe13s27);
if v < 0 then begin // 負数の立方根対策
v := power(-v, 1/3);
v := -v;
end
else v := power(v, 1/3);
wiupv := u + v;
end
else begin
r := sqrt(e02s4 + ABS(e02s4pe13s27)); // r > 0 e02s4 は必ずプラスかゼロなのでゼロ以下は無し
rh1s3 := power(r , 1/3);
if r <> 0 then begin
cosQ := -e0s2 / r;
Q := arccos(cosQ);
cosQs3 := cos(Q / 3);
sinQs3 := sin(Q / 3);
wiupv := 2 * rh1s3 * cosQs3;
u := rh1s3 * cosQs3;
v := u;
end
else
wiupv := 0;
end;
t := wiupv - 2 / 3 * b2; // t > 0
if t < 0 then t := 0;
c1 := sqrt(t);
if c1 <> 0 then c0 := (c1 * c1 * c1 + b2 * c1 - b1) / 2 / c1
else
if b2 * b2 - 4 * b0 > 0 then
c0 := (b2 + sqrt(b2 * b2 - 4 * b0)) / 2
else
c0 := b2 / 2;
d1 := - c1;
d0 := b0 / c0;
end
else begin
c1 := 0;
c0 := (b2 + sqrt(t)) / 2;
d1 := 0;
d0 := (b2 - sqrt(t)) / 2
end;
if e02s4pe13s27 < 0 then begin
up := floatTostr(rh1s3 * sinQs3) + ' i'; // 複素数処理 textに変換
vm := floatTostr(rh1s3 * sinQs3) + ' i'; // 複素数処理 textに変換
end;
c1h2s4mc0 := c1 * c1 / 4 - c0;
d1h2s4md0 := d1 * d1 / 4 - d0;
if abs(c1h2s4mc0) < KXYE then c1h2s4mc0 := 0; // 計算誤差の許容 +-0.0001 以下
if abs(d1h2s4md0) < KXYE then d1h2s4md0 := 0; // 計算誤差の許容 +-0.0001 以下
if c1h2s4mc0 >=0 then begin
x1 := -c1 / 2 - A3 / 4 + sqrt(c1h2s4mc0); // x1
Result := Result or 1;
x2 := -c1 / 2 - A3 / 4 - sqrt(c1h2s4mc0); // x2
Result := Result or 2;
end
else begin
x1 := -c1 / 2 - A3 / 4; // x1
xim1 := ' + ' + floatTostr(sqrt(-c1h2s4mc0)) + ' i'; // 複素数処理 textに変換
x2 := -c1 / 2 - A3 / 4; // x2
xim2 := ' - ' + floatTostr(sqrt(-c1h2s4mc0)) + ' i'; // 複素数処理 textに変換
end;
if d1h2s4md0 >= 0 then begin
x3 := -d1 / 2 - A3 / 4 + sqrt(d1h2s4md0); // x3
Result := Result or 4;
x4 := -d1 / 2 - A3 / 4 - sqrt(d1h2s4md0); // x4
Result := Result or 8;
end
else begin
x3 := -d1 / 2 - A3 / 4; // x3
xim3 := ' + ' + floatTostr(sqrt(-d1h2s4md0)) + ' i'; // 複素数処理 textに変換
x4 := -d1 / 2 - A3 / 4; // x4
xim4 := ' - ' + floatTostr(sqrt(-d1h2s4md0)) + ' i'; // 複素数処理 textに変換
end;
image2.Canvas.TextOut(20, 110,'x1= ' + floattostr(x1) + ' ' + xim1);
image2.Canvas.TextOut(20, 125,'x2= ' + floattostr(x2) + ' ' + xim2);
image2.Canvas.TextOut(20, 140,'x3= ' + floattostr(x3) + ' ' + xim3);
image2.Canvas.TextOut(20, 155,'x4= ' + floattostr(x4) + ' ' + xim4);
image2.Canvas.TextOut(20, 170, 'u= ' + floattostr(u) + ' + ' + up);
image2.Canvas.TextOut(20, 185, 'v= ' + floattostr(v) + ' - ' + vm);
end;
// 二次方程式の解法
if (abs(a) <= MINIMAM) and (abs(c) > 0) then begin // cの値が小さいので abs(c) > MINIMAM を abs(c) > 0 に変更
a0 := c; // Bxy をゼロにした場合の影響のようです。
b0 := d;
c0 := e;
f0 := b0 * b0 - 4 * a0 * c0;
if f0 < 0 then
if abs(f0) < KXYE then f0 := 0; // 誤差1E-9 は許容
if f0 >= 0 then begin
X1 := (-b0 + sqrt(f0)) / 2 / a0;
X2 := (-b0 - sqrt(f0)) / 2 / a0;
result := 1 + 2;
end
else begin
x1 := -b0 / a0 / 2;
x2 := x1;
xim1 := floattostr( sqrt(abs(f0) / a0 / 2)) + ' i';
xim2 := floattostr(- sqrt(abs(f0) / a0 / 2)) + ' i';
end;
with image2.Canvas do begin
TextOut(20, 110,'x1= ' + floattostr(x1) + ' ' + xim1);
TextOut(20, 125,'x2= ' + floattostr(x2) + ' ' + xim2);
end;
end;
image2.Canvas.TextOut(10, 95,'４次式の解法結果');
end;
//-------------------------------------------
// 楕円1の Xo1, Xo2 を原点として
// 座標変換されているので元の座標にも戻します
//-------------------------------------------
procedure TForm1.trance(Xn, Yn, defQ, xo1, yo1: Extended; var x, y: Extended);
var
xh, yh : Extended;
stn : Extended;
Q, Q1 : Extended;
begin
Q := arctan2(Yn, Xn);
Q1 := Q - defQ;
stn := sqrt(xn * xn + yn * yn);
xh := cos(Q1) * stn;
yh := sin(Q1) * stn;
x := xh + xo1;
y := yh + yo1;
end;
//------------------------
// saq を 0～dq に修正
//-----------------------
function TForm1.anglecheck(saq, dq: Extended): Extended;
begin
repeat
if saq >= dq then saq := saq - dq;
if saq < 0 then saq := saq + dq;
until (saq >= 0) and (saq < dq);
result := saq;
end;
//--------------------------------------------------------------------------------------
// 二つの楕円の交点計算
// Bxyがゼロになる楕円の二次式を求めてから、Cy^2をゼロにして四次式を解法しています。
// 二つの楕円の二元二次式からBxyがゼロになる様に差分の二元二次式を計算し、
// その二元二次式から通常の楕円関数を求めると、半径が虚数になる場合があります。
// 半径が虚数になっても、交点は正しく求める事が出来ます。
// 此処の計算では、半径が虚数にならない様に、楕円の座標変換をしてから計算することもできます。
// 差分の二元二次式から求めた楕円関数の半径の値が非常に大きくなることがあります。
// Bxyの値がゼロの場合の楕円の角度は0°か90°になります。
//--------------------------------------------------------------------------------------
function TForm1.cross_calc: boolean;
label
REDEF;
const
Ftop = 260;
k180 = 180;
k90 = 90;
FIMIN = 1.0E-8;
K1E4 = 10000;
var
x1, x2, x3, x4 : Extended;
y1, y2, y3, y4 : Extended;
A1, B1, C1, D1, E1, F1 : Extended;
A2, B2, C2, D2, E2, F2 : Extended;
A3, B3, D3, E3, F3 : Extended;
A4, B4, C4, D4, E4, F4 : Extended;
A, B, C, D, E : Extended;
xflag : byte;
qb, qn : Extended;
nx, ny : Extended;
stn : Extended;
sq, tmq : Extended;
xob, yob : Extended;
q1b, q2b : Extended;
Xs, Ys, Ars, Brs, Qs : Extended;
qc1, qc2 : Extended;
trnQ : Extended;
dqs, Qj : Extended;
czeroF : boolean;
ratioF : Boolean;
I : integer;
Chfd : array[0..3] of boolean;
// Cy^2 を消去した式にxの値を入れてyの値計算
// Y = (Ax^2 + Dx + F) / (Bx + E)
function ansy(x: Extended): Extended;
begin
result := - (A3 * x * x + D3 * x + F3) / (B3 * x + E3);
end;
// 楕円の二元二次式に
// xとyの値を入れて計算 ゼロから外れていればx,yは楕円上にありません
function czerosub(x, y: Extended): Extended;
begin
result := abs(A1 * x * x + B1 * x * y + C1 * y * y + D1 * x + E1 * y + F1);
result := result + abs(A2 * x * x + B2 * x * y + C2 * y * y + D2 * x + E2 * y + F2);
end;
// 座標値表示 計算原点が楕円1なので修正
procedure textxy(x, y: Extended; px, py:integer; str: string; TCF : boolean);
var
CT : Tcolor;
begin
x := (x + xb1) / scale;
y := (y + yb1) / scale;
CT := image2.Canvas.Font.Color;
if not TCF then image2.Canvas.Font.Color := clRed;
image2.Canvas.TextOut( px, py ,'x' + str + '= ' + floatTostrF(x,ffFixed,10,6));
image2.Canvas.TextOut( 200 + px, py ,'y' + str + '= ' + floatTostrF(y,ffFixed,10,6));
image2.Canvas.Font.Color := CT;
end;
// 交点丸表示 誤差の大きいところは赤丸表示
procedure crosspront(x, y: Extended; PCF: boolean);
var
CP : Tcolor;
begin
if PCF then CP := clblack
else CP := clred;
EllipseEx(image1.Canvas, image1.Height, 3, 1, CP,
5, 5,
(x - shift_x) * magnification + draw_margin,
(y - shift_y) * magnification + draw_margin,
0,
0, 360);
end;
begin
// 左右対称の角度と 0度、90度の角度を避けて
// 計算します。
// sq 補正角度
qc1 := q1;
if q1 > k90 then qc1 := q1 - k180;
qc2 := q2;
if q2 > k90 then qc2 := q2 - k180;
trnQ := 0;
QS := 0;
Qj := 0;
// 左右、上下対称な角度だったら 対象から避けます
if round(qc1) = round(-qc2) then begin
// 角度を２度づつ加算 両方の絶対値がゼロかゼロより大きくなったら
Repeat
trnQ := trnQ + 2;
qc1 := qc1 + 2;
qc2 := qc2 + 2;
until (abs(qc1) >= 0) and (abs(qc2) >= 0);
// 補正角度の絶対値で補正角度選択
if abs(qc1) > abs(qc2) then Qs := abs(qc1)
else Qs := abs(qc2);
sq := trnQ + Qs;
end
else sq := 0;
// 何方かの角度が90°だったら90°からずらします
if (round(q1) = k90) or (round(q2) = k90) then begin
trnQ := q1 - 2;
tmq := q1;
// q1又はq2の角度から、0～90°の範囲の角度にします
// 補正角度を小さくするためです
tmq := anglecheck(tmq, k90);
// 角度差
sq := trnQ - tmq;
end;
// q1 がゼロ度だったら
if (Trunc(q1) = 0) and (round(q2) <> 0) and (Qs = 0) then begin
if (round(q2) - 2 > 2) and (round(q2) - 2 <> k90) then trnQ := q1 - 2
else trnQ := q1 + 2;
tmq := q1;
// q1角度から、0～90どの範囲の角度にします
// 補正角度を小さくするためです
tmq := anglecheck(tmq, k90);
// 角度差
sq := trnQ - tmq;
end;
// q2 がゼロ度だったら
if (round(q1) <> 0) and (Trunc(q2) = 0) and (Qs = 0) then begin
if (round(q1) - 2 > 2) and (round(q1) - 2 <> k90) then trnQ := q2 - 2
else trnQ := q2 + 2;
tmq := q2;
// q2の角度から、0～90どの範囲の角度にします
// 補正角度を小さくするためです
tmq := anglecheck(tmq, k90);
// 角度差
sq := trnQ - tmq;
end;
// 二つの楕円の半径比と角度が等しい場合Bxyをゼロにすると交点が計算できないので
// Bxyをゼロにする計算をしない為のフラグ設定。
// 二つの楕円の半径比と角度が等しい場合でBxyをゼロにする計算をすると
// 計算された結果は Ax^2 = 0, Bxy = 0, Cy^2 = 0 となり
// Dx + Ey + F = 0 の一次式になります。 y = (F + Dx) / -E
// どちらかの楕円に代入して、二次方程式の解法を行えば交点がえられます。
// A と C の値には計算誤差があるので完全にはゼロになりません。
// そこで、A と C の絶対値値がどれぐらい小さい値になったら一次式とするか
// 判別する必要があります。
// このプログラムでは、Bxyをゼロにする計算をしないで避けています。
// その場合は四次式の解法時二次式として解法されます。
ratioF := true;
if not firstbox.Checked then begin
if round(ar1 / br1 * K1E4) = round(ar2 / br2 * K1E4) then
if round((q1 - q2) * K1E4) = 0 then ratioF := False;
// 90°違う場合
if round(ar1 / br1 * K1E4) = round(br2 / ar2 * K1E4) then
if round(abs(q1 - q2) * K1E4) = round(k90 * K1E4) then ratioF := False;
end;
nx := xo2 - xo1; // 楕円X方向距離
ny := yo2 - yo1; // 楕円Y方向距離
REDEF:
// 楕円１と２の位置の角度補正値計算 座標変換に使用します。
dfQ := sq /180 * pi;
qb := arctan2(ny, nx);
qn := qb + dfQ;
// 楕円１と２の角度補正
q2b := q2 + sq;
q1b := q1 + sq;
// 0～180°の範囲になるように修正
q2b := anglecheck(q2b, k180);
q1b := anglecheck(q1b, k180);
// 補正した角度が90°だったら補正角１°マイナス
if (round(q1b) = k90) or (round(q2b) = k90) then begin
sq := sq + 1;
goto REDEF; // 補正角設定へ戻り
end;
// 楕円２の新しい中心座標計算
stn := sqrt(nx * nx + ny * ny);
xob := cos(qn) * stn;
yob := sin(qn) * stn;
// 楕円式の変換 二次方程式に変換
quadratic_transform(ar1, br1, 0, 0, q1b, A1, B1, C1, D1, E1, F1);
quadratic_transform(ar2, br2, xob, yob, q2b, A2, B2, C2, D2, E2, F2);
A4 := A2; B4 := B2; C4 := C2; D4 := D2; E4 := E2; F4 := F2;
// 軸角がゼロで無かったらB(XY)がゼロになる様に差分計算
// (0と90°にならない様に角度を設定してB1,B2がゼロにならない様にしていますが
// 念のため確認をしています)
// 円はBの値がゼロになります。
if NoXYBox.Checked and ratioF then
if (B2 <> 0) and (B1 <> 0) then begin
B3 := B1 / B2; // B1 - B2 * B3 がゼロになるB3の値計算
if abs(C1 - C2 * B3) > 0 then begin // C1 - C2 * B3 がゼロで無い場合差分計算
A4 := A1 - A2 * B3; // ゼロだとCy^2が最初から０となり次の
C4 := C1 - C2 * B3; // Cy^2をゼロにする計算が成り立たないので
D4 := D1 - D2 * B3; // 差分計算をしません。
E4 := E1 - E2 * B3;
F4 := F1 - F2 * B3;
B4 := 0;
// 計算開始時半径比と角度の確認をしなかった場合此処で確認します。
if firstbox.Checked then begin
// A4とC4が非常に小さく無視できる場合は一次式と等価になるので戻します。
// 一次式 D4x + E4y + F4 = 0
// この場合は何方かの楕円に代入すれば答えが得られますが此処では計算しません。
// 元へ戻します。
if (abs(A4) < FIMIN) and (abs(C4) < FIMIN) then begin
A4 := A2; B4 := B2; C4 := C2; D4 := D2; E4 := E2; F4 := F2;
ratioF := False;
end;
end;
end;
end;
// 楕円式に変換 楕円にならず半径が虚数になる場合が有り 交点は求まりますが
// 一応虚数を避けるか避けないか指定が出来ます。
// Qj は 0 か 90°-90°になります。
if NoXYBox.Checked and ratioF then
// 半径が虚数の時 False
if not elementsCalc(A4, B4, C4, D4, E4, F4, Xs, Ys, Ars, Brs, Qj) then begin
// 虚数を避けない場合双曲線作図します。
if checkbox2.Checked then begin
hyperbola(A4, B4, C4, D4, E4, F4, sq / k180 * pi); // 双曲線作図
end
// 虚数を避ける場合虚数で無くなるまで補正角を変更します。
else begin
sq := sq + 1; // 半径が虚数だったら補正値1゛加算
// 楕円同士の中心角度を避けます。
dqs := qb / pi * k180 + sq;
dqs := round(anglecheck(dqs, k90)); // 0°と90°の時ゼロ
// 1°を加算後補正角が90°と一致したら更に1°度加算
if dqs = 0 then sq := sq + 1;
if sq < 90 then goto REDEF; // 補正角設定へ戻り 90度を超えたら打ち切り
end;
end
else
image2.Canvas.TextOut(30, 415, '0xy角度 Qj＝ ' + floatTostrF(Qj, ffGeneral, 10, 3)+'°');
image2.Canvas.TextOut(10, 435, '交点計算時の座標変換角度');
Qs := Qs - sq; // 作図補正角設定
Qs := anglecheck(Qs, k180); // Qs 0～180°
image2.Canvas.TextOut(20, 450, '補正角 sq ＝ ' + floatTostrF(sq, ffGeneral, 10, 3)+'°');
image2.Canvas.TextOut(20, 465, '作図補正 Qs ＝ ' + floatTostrF(Qs, ffGeneral, 10, 3)+'°');
if not ratioF and NoXYBox.Checked then image1.Canvas.TextOut(400, 0,'楕円比と角度が等しいので Bxyゼロ式不可です。');
// 原点座標に変換
trance(Xs, Ys, dfQ, xo1, yo1, Xs, Ys);
// Bxy = 0 の新しい楕円の作図
Xs := (Xs - shift_x) * magnification + draw_margin;
Ys := (Ys - shift_y) * magnification + draw_margin;
if NoXYBox.Checked and ratioF then
EllipseEx(image1.Canvas, image1.Height, 3, 1, clGreen,
Ars * magnification, Brs * magnification,
Xs, Ys,
Qj- sq, // 楕円中心位置角がsq分加算して計算されるので、作図時はsq分戻して作図します。
0, 360);
// Cy^2 の消去
A3 := A1 / C1 - A4 / C4;
B3 := B1 / C1 - B4 / C4;
D3 := D1 / C1 - D4 / C4;
E3 := E1 / C1 - E4 / C4;
F3 := F1 / C1 - F4 / C4;
// A3x^2 + B3xy + D3x + E3y + F3 = 0
// y = - (A3x^2 + D3x + F3)/(B3x + E3)
// y 二次曲線作図
if CY2ZeroBox.Checked then Secondary_curve(A3, B3, D3, E3, F3, sq / 180 * pi);
// 四次式の係数を求めます
// Ax^4 + Bx^3 + Cx^2 + Dx + E = 0;
A := A1*B3*B3 - A3*B1*B3 + A3*A3*C1;
B := 2*A1*B3*E3 + 2*A3*C1*D3 + B3*B3*D1 - A3*B1*E3 - B1*B3*D3 - A3*B3*E1;
C := A1*E3*E3 + 2*A3*C1*F3 + D3*D3*C1 + 2*B3*D1*E3 + B3*B3*F1 - B1*B3*F3
- B1*D3*E3 - A3*E1*E3 - B3*D3*E1;
D := 2*C1*D3*F3 + D1*E3*E3 + 2*B3*E3*F1 - B3*E1*F3 - D3*E1*E3 - B1*E3*F3;
E := C1*F3*F3 + E3*E3*F1 - E1*E3*F3;
image2.Canvas.Brush.Style := bsClear;
// 連立方程式の係数表示 ;
image2.Canvas.TextOut(10, 5, '４次式 Ax^4 + Bx^3 + Cx^2 + Dx + E = 0');
image2.Canvas.TextOut(20, 20, 'A= ' + floatTostr(A));
image2.Canvas.TextOut(20, 35, 'B= ' + floatTostr(B));
image2.Canvas.TextOut(20, 50, 'C= ' + floatTostr(C));
image2.Canvas.TextOut(20, 65, 'D= ' + floatTostr(D));
image2.Canvas.TextOut(20, 80, 'E= ' + floatTostr(E));
image2.Canvas.TextOut(10, 200, 'Cy^2 消去後のBxy, Ey');
image2.Canvas.TextOut(20, 215, 'B3= ' + floatTostr(B3));
image2.Canvas.TextOut(20, 230, 'E3= ' + floatTostr(E3));
image2.Canvas.TextOut(10, 485, '計算時の楕円の角度' + floatTostr(q1b));
image2.Canvas.TextOut(20, 500, 'q1b= ' + floatTostr(q1b));
image2.Canvas.TextOut(20, 515, 'q2b= ' + floatTostr(q2b));
result := false;
xflag := 0;
// 連立方程式の解放を行い x の値を計算 x の値から
// y の値を求めます 分母がゼロ場合は計算しません 分母 B3x + E3
// 四次 二次式の解法
if (B3 <> 0) or (E3 <> 0) then
xflag := cross_quadratic(a, b, c, d, e, x1, x2, x3, x4);
// y の値を求めます x が虚数の場合は計算しません
// B3x + E3 がゼロより大きい場合は四次方程式作成に利用した
// yの値を求める式でyの値を計算します
if xflag <> 0 then begin
if xflag and 1 = 1 then begin
if abs(B3 * x1 + E3) > 0 then y1 := ansy(x1)
else xflag := xflag and ($FF - 1);
end;
if xflag and 2 = 2 then begin
if abs(B3 * x2 + E3) > 0 then y2 := ansy(x2)
else xflag := xflag and ($FF - 2);
end;
if xflag and 4 = 4 then begin
if abs(B3 * x3 + E3) > 0 then y3 := ansy(x3)
else xflag := xflag and ($FF - 4);
end;
if xflag and 8 = 8 then begin
if abs(B3 * x4 + E3) > 0 then y4 := ansy(x4)
else xflag := xflag and ($FF - 8);
end;
end
else result := true;
// 計算結果が楕円上かどうか確認します。
czeroF := True;
for I := 0 to 3 do Chfd[I] := true;
if xflag and 1 = 1 then
if czerosub(x1, y1) > KCCH then begin
czeroF := False;
Chfd[0] := False;
end;
if xflag and 2 = 2 then
if czerosub(x2, y2) > KCCH then begin
czeroF := False;
Chfd[1] := False;
end;
if xflag and 4 = 4 then
if czerosub(x3, y3) > KCCH then begin
czeroF := False;
Chfd[2] := False;
end;
if xflag and 8 = 8 then
if czerosub(x4, y4) > KCCH then begin
czeroF := False;
Chfd[3] := False;
end;
// 楕円上でない場合で 半径虚数使用の場合は補正角の修正で計算精度が高くなる
// 事を期待して補正角1°変更再計算します。
if checkbox2.Checked then
if not czeroF then begin
inputdata_drawing; // 入力楕円図再描画
sq := sq + 1; // 補正値1゛加算
if sq < 90 then goto REDEF; // 補正角設定へ戻り
end;
image2.Canvas.TextOut(10, Ftop - 15, '交点の座標');
// 計算結果の表示 座標は元の座標に戻します
if xflag and 1 = 1 then begin
trance(X1, Y1, dfQ, xo1, yo1, x1, y1); // 座標変換 原点座標に戻します。
textxy(x1, y1, 20, Ftop, '1', Chfd[0]); // 値表示 楕円１の座標を加算して表示します。
crosspront(x1, y1, Chfd[0]); // 交点丸表示
end;
if xflag and 2 = 2 then begin
trance(X2, Y2, dfQ, xo1, yo1, x2, y2);
textxy(x2, y2, 20, Ftop + 15, '2', Chfd[1]);
crosspront(x2, y2, Chfd[1]);
end;
if xflag and 4 = 4 then begin
trance(X3, Y3, dfQ, xo1, yo1, x3, y3);
textxy(x3, y3, 20, Ftop + 30, '3', Chfd[2]);
crosspront(x3, y3, Chfd[2]);
end;
if xflag and 8 = 8 then begin
trance(X4, Y4, dfQ, xo1, yo1, x4, y4);
textxy(x4, y4, 20, Ftop + 45, '4', Chfd[3]);
crosspront(x4, y4, Chfd[3]);
end;
if not czeroF then begin
if not crosspBox.Checked then begin
timF := False;
Timer1.Enabled := False;
end;
image1.Canvas.TextOut(20, 500,'交点の計算誤差が大きく正しく計算できませんでした。');
end;
end;
//--------------------------------------------------------
// 入力された楕円の描画
// 楕円作図のy方向は、楕円作図ルーチンで修正されます。
//--------------------------------------------------------
procedure TForm1.inputdata_drawing;
var
all_width, all_height : Extended;
ac1, ac2 : Extended;
x1, x2, y1, y2 : Extended;
left_min, left_max : Extended;
top_min, top_max : Extended;
begin
// 楕円の半径の大きい方選択
ac1 := ar1;
if ar1 < br1 then begin
ac1 := br1;
end;
ac2 := ar2;
if ar2 < br2 then begin
ac2 := br2;
end;
// 作図範囲の設定
left_min := xo1 - ac1;
if xo2 - ac2 < left_min then left_min := xo2 - ac2;
left_max := xo1 + ac1;
if xo2 + ac2 > left_max then left_max := xo2 + ac2;
all_width := left_max - left_min;
top_min := yo1 - ac1;
if yo2 - ac2 < top_min then top_min := yo2 - ac2;
top_max := yo1 + ac1;
if yo2 + ac2 > top_max then top_max := yo2 + ac2;
all_height := top_max - top_min;
top_max := (image1.Height - draw_margin * 2) / all_Height;
magnification := (image1.Width - draw_margin * 2) / all_width;
if magnification > top_max then magnification := top_max;
shift_x := left_min;
shift_y := top_min;
// イメージクリア
imageClear;
// 楕円作図 作図中心座標
x1 := (xo1 - left_min) * magnification + draw_margin;
y1 := (yo1 - top_min) * magnification + draw_margin;
x2 := (xo2 - left_min) * magnification + draw_margin;
y2 := (yo2 - top_min) * magnification + draw_margin;
// 楕円１作図
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
3, // 線種
1, // 線幅
clRed, // 色
ar1 * magnification, // 半径a
br1 * magnification, // 半径b
x1, // 中心位置x
y1, // 中心位置y
q1, // 回転角 deg
0, // 作図開始角
360); // 作図終了角
// 楕円２作図
EllipseEx(image1.Canvas, image1.Height, 3, 1, clBlue,
ar2 * magnification, br2 * magnification,
x2, y2,
q2,
0, 360);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed, x1 - 30, y1, x1 + 30, y1, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed, x1, y1 - 30, x1, y1 + 30, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue, x2 - 30, y2, x2 + 30, y2, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue, x2, y2 - 30, x2, y2 + 30, true);
end;
//-------------------
// 交点計算計算開始
//-------------------
procedure TForm1.SelectBtnClick(Sender: TObject);
const
k180 = 180; // 180°
K200 = 200; // 基準半径
K1E4 = 1.0E4; // 10000
var
ch : integer;
ar1in, br1in : Extended;
ar2in, br2in : Extended;
xb1in, yb1in : Extended;
xb2in, yb2in : Extended;
Mr : Extended;
begin
// 端数加算チェック
val(pEdit.Text, Mr, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('端数加算が数値ではありません。', '端数加算', 0);
exit;
end;
if abs(Mr) >= 1 then begin
timF := False;
application.MessageBox('端数加算の値を小数点以下の値にして下さい。', '端数加算', 0);
exit;
end;
// 楕円１のデーター
val(radius_a1_Edit.Text, ar1in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円１の半径a１数値ではありません。', '楕円１の半径a１', 0);
exit;
end;
if ar1in <= 0 then begin
timF := False;
application.MessageBox('楕円１の半径a１がゼロ 又はゼロ以下です。', '楕円１の半径a１', 0);
exit;
end;
val(radius_b1_Edit.Text, br1in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円１の半径b１数値ではありません。', '楕円１の半径b１', 0);
exit;
end;
if br1in <= 0 then begin
timF := False;
application.MessageBox('楕円１の半径b１がゼロ 又はゼロ以下です。', '楕円１の半径b１', 0);
exit;
end;
val(Center_x1_Edit.Text, xb1in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円１の中心位置x１数値ではありません。', '楕円１の中心位置x１', 0);
exit;
end;
val(Center_y1_Edit.Text, yb1in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円１の中心位置y１数値ではありません。', '楕円１の中心位置y１', 0);
exit;
end;
val(angle_q1_Edit.Text, q1, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円１の角度θ１数値ではありません。', '楕円１の角度θ１', 0);
exit;
end;
// 楕円２のデーター
val(radius_a2_Edit.Text, ar2in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円２の半径a２数値ではありません。', '楕円２の半径a２', 0);
exit;
end;
if ar2in <= 0 then begin
timF := False;
application.MessageBox('楕円２の半径a２がゼロ 又はゼロ以下です。', '楕円２の半径a２', 0);
exit;
end;
val(radius_b2_Edit.Text, br2in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円２の半径b２数値ではありません。', '楕円２の半径b２', 0);
exit;
end;
val(Center_x2_Edit.Text, xb2in, ch);
if br2in <= 0 then begin
timF := False;
application.MessageBox('楕円２の半径b２がゼロ 又はゼロ以下です。', '楕円２の半径b２', 0);
exit;
end;
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円２の中心位置x２数値ではありません。', '楕円２の中心位置x２', 0);
exit;
end;
val(Center_y2_Edit.Text, yb2in, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円２の中心位置y２数値ではありません。', '楕円２の中心位置y２', 0);
exit;
end;
val(angle_q2_Edit.Text, q2, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('楕円２の角度θ２数値ではありません。', '楕円２の角度θ２', 0);
exit;
end;
val(KcchEdit.Text, KCCH, ch);
if ch <> 0 then begin
timF := False;
application.MessageBox('交点誤差判定値が数値ではありません。', '交点誤差判定値', 0);
exit;
end;
if KCCH <= 0 then begin
timF := False;
application.MessageBox('交点誤差判定値がゼロかマイナス値です。', '交点誤差判定値', 0);
exit;
end;
// 計算の安定化の為楕円の最大半径を一定の値に変換します。
// 最大半径検索
Mr := ar1in;
if br1in > Mr then Mr := br1in;
if ar2in > Mr then Mr := ar2in;
if br2in > Mr then Mr := br2in;
scale := K200 / Mr;
// 入力値の補正
ar1 := ar1in * scale;
br1 := br1in * scale;
ar2 := ar2in * scale;
br2 := br2in * scale;
xb1 := xb1in * scale;
yb1 := yb1in * scale;
xb2 := xb2in * scale;
yb2 := yb2in * scale;
// 楕円の角度は、一回転180°なので、180°以下にします
q1 := anglecheck(q1, k180);
q2 := anglecheck(q2, k180);
// 楕円１の中心を原点に移動します
xo1 := 0;
yo1 := 0;
xo2 := xb2 - xb1;
yo2 := yb2 - yb1;
inputdata_drawing; // 楕円表示
// 完全に同じ楕円の場合は計算しません。
// 小数点4桁以下は無視します。
if (round(ar1 * K1E4) = round(ar2 * K1E4)) and
(round(br1 * K1E4) = round(br2 * K1E4)) and
(round(q1 * K1E4) = round(q2 * K1E4)) and
(round(xo1 * K1E4) = round(xo2 * K1E4)) and
(round(yo1 * K1E4) = round(yo2 * K1E4)) then exit;
// 交点が正しく計算できなかったらエラー表示
if cross_calc then begin
if not EchkBox.Checked then begin
timF := False;
Timer1.Enabled := False;
end;
image1.Canvas.TextOut(20, 530,'交点を計算できませんでした。');
end;
end;
var
NextF : boolean;
stepF : boolean;
//------------------
// 自動ループ計算
//------------------
procedure TForm1.AutoCheckRoot;
const
K180 = 180;
var
I : integer;
M, N : integer;
inf : Extended;
begin
val(angle_q1_Edit.Text, inf, I);
if I <> 0 then begin
application.MessageBox('楕円１の角度θ１数値ではありません。', '楕円１の角度θ１', 0);
exit;
end;
N := Trunc(inf);
val(angle_q2_Edit.Text, inf, I);
if I <> 0 then begin
application.MessageBox('楕円２の角度θ２数値ではありません。', '楕円２の角度θ２', 0);
exit;
end;
M := Trunc(inf);
repeat
if checkBox1.Checked = true then angle_q1_Edit.Text := IntTostr(M) + pEdit.Text
else angle_q2_Edit.Text := IntTostr(M) + pEdit.Text;
repeat
NextF := False;
if checkBox1.Checked = true then angle_q2_Edit.Text := IntTostr(N) + pEdit.Text
else angle_q1_Edit.Text := IntTostr(N) + pEdit.Text;
TimF := False;
if Timer1.Enabled then TimF := True;
Timer1.Enabled := False;
application.ProcessMessages;
SelectBtn.Click; // 交点計算
if TimF then Timer1.Enabled := True;
application.ProcessMessages;
repeat
sleep(1);
application.ProcessMessages;
if not Timer1.Enabled then exit;
until NextF and stepF;
inc(N);
until N > 179;
N := 0;
Inc(M);
until M > 179;
angle_q2_Edit.Text := IntTostr(0);
angle_q1_Edit.Text := IntTostr(0);
Timer1.Enabled := False;
panel1.Enabled := true;
end;
//------------------------------
// 自動ループ計算用タイマー
//------------------------------
procedure TForm1.Timer1Timer(Sender: TObject);
begin
NextF := True;
end;
//----------------------------------
// 自動ループ計算スタートストップ
//----------------------------------
procedure TForm1.AutoBtnClick(Sender: TObject);
begin
if not stepF then begin
stepF := True;
Timer1.Enabled := false;
end;
if not Timer1.Enabled then begin
timer1.Enabled := true;
panel1.Enabled := false;
StepBtn.Enabled := true;
end
else begin
timer1.Enabled := false;
panel1.Enabled := true;
StepBtn.Enabled := false;
end;
if timer1.Enabled then AutoCheckRoot;
end;
//-----------
// 一時停止
//-----------
procedure TForm1.StepBtnClick(Sender: TObject);
begin
if not stepF then begin
stepF := True;
panel1.Enabled := false;
AutoBtn.Enabled := true;
end
else begin
stepF := False;
panel1.Enabled := true;
AutoBtn.Enabled := false;
end;
end;
//-----------
// 初期設定
//-----------
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // １点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // ２点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
// イメージクリア
imageClear;
image2.Canvas.Font.Name := 'ＭＳ ゴシック';
// image2.Canvas.Font.Style := [fsbold];
image2.Canvas.Font.Height := 13;
StepBtn.Enabled := false;
end;
end.
EllipsesNodeXYzero.zip